―― 連成振動 ―― (I) ３質点による連成振動 　直線上において、バネで連結した３つの質点の運動を考える。質点の質量はすべて ｍ、 バネ定数はすべて ｋ とし、 両端のバネは図のように固定されているとする。 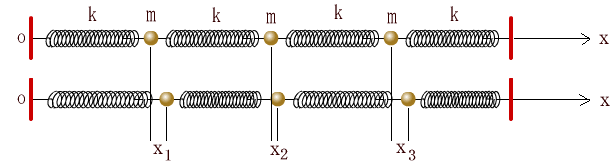　　　　 　運動方程式は次のようになる。 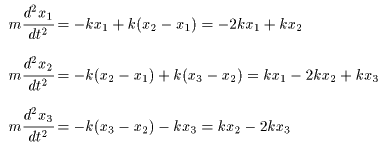　　　　 　上式は、行列を用いて次のように表示される。 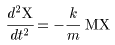　　　　 ここで、 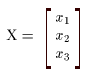　　　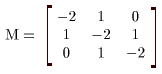　,　　　　 である。 　行列 M の固有値は 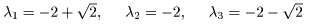　　　　 である。 M は、行列 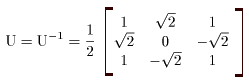　　　　 によって、次のように対角化される。 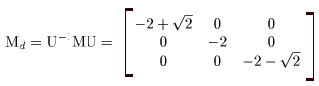　　　　 　したがって、運動方程式は次のように書かれる。 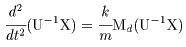　　　　 　さて、上式の各成分をみると、それぞれ 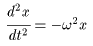　　　　 の形の微分方程式になっている。よく知られているように、この微分方程式の一般解は Ａ, α を任意定数として、 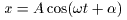　　　　 である。よって、 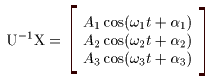　　　　 ここで 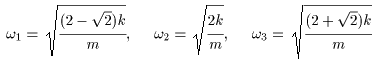　　　　 のように一般解が得られ、さらに次式が得られる。 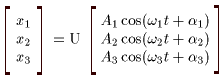　　　　 ここで、Ａj, αj　 ( j = 1,2,3 ) は任意定数で、初期条件により定められるべきものである。 (�U) 多質点による連成振動（リング模型） 　（Ｉ）で議論した３つの質点の場合を拡張してみよう。 直線上において、バネで連結したｎ個の質点の運動を考える。質点の質量はすべて ｍ、 バネ定数はすべて ｋ とし、 両端のバネは固定されているとする。 　運動方程式は次のようになる。 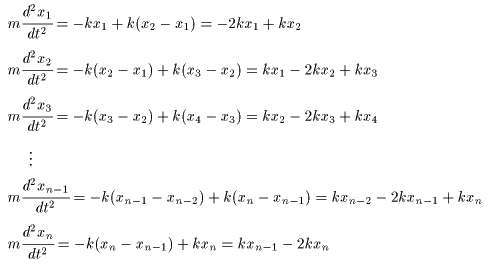　　　　 　上式は、行列を用いて次のように表示される。 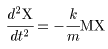　　　　 ここで、 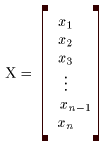　　　　,　　　　 である。 　３つの質点の場合と同様に、行列 M を対角化して同様の議論を展開すればよいのであるが、少々面倒である。そこで、ここでは次のようにする。 　このモデルでは、質点とバネは一直線上にあるが、ｎが充分大きいとして、リング状にする。すなわち、最後のｎ番目の質点に付けられていたバネを取り外し、１番目の質点に取り付けられているバネの他端をｎ番目の質点に取り付けリング状にする。ｎは充分に大きいので、局部的にみれば各質点は直線状で運動するとしてよい。 　このモデルでは、行列 M が次にようになる。この行列は次で示すように、容易に対角化される。 　　　　 　いま、次の行列 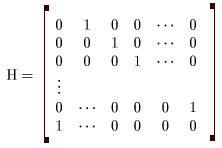　　　　 を導入する。この行列については 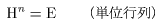　　　　 が成立する。 固有値は λn=1 のｎ個の解である。すなわち、 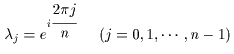　　　　 で与えられる。また、Hを対角化する行列は 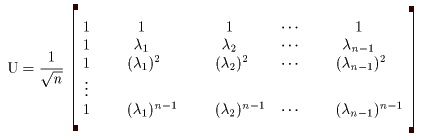　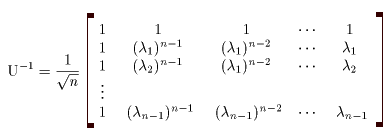　　　 　　　　 で、次のようになる。 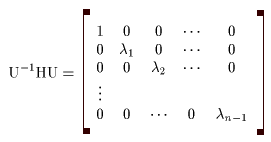　　　　 　ところで、 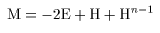　　　　 であるから、M は U で次のように対角化される。 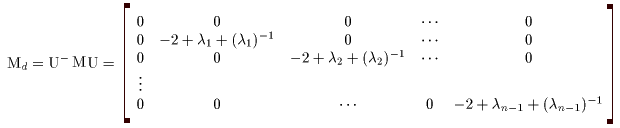　　　　 　したがって、運動方程式は次のように書かれる。 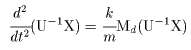　　　　 　（I)での議論と同様にして一般解として次式を得る。 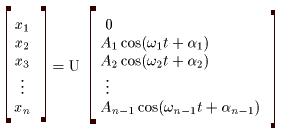　　　　 ここで、 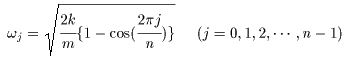　　　　 である。また、Ａj, αj　 ( j = 1,2,…,n-1 ) は任意定数で、初期条件により定められるべきものである。 Copyright(C) 2006 YokahiYokatoki