「三目並べ」は、〇が先手、×が後手で、一手づつ交代で打って縦、横、斜めのいづれかに３つ
	先に並べた方が勝ちというゲームです。
	　ここでは、種々の戦法で、コンピュータ同士で対局させ、その戦法の良し悪しを比較してみ
	ることが目的です。
	　なお、互いが最善手を打ったならば、引分けになることが分かっています。

	用いる戦法は、
	　完全探索(αβ法)、ランダム、原始モンテカルロ探索、モンテカルロ木探索
	です。
	

	(1) 完全探索(αβ法)
	　このゲームは、９手以内で勝敗がつきます。勝敗がつくまで完全探索を行い、常に最善手を見
	出して打ちます。したがって、両者とも完全探索によって対局すると、100% 引分けになります。
	また、相手が完全探索以外の戦法を用いた場合には、勝つか引分けになり、負けることはありま
	せん。

	(2) ランダム
	　そのとき打つことができる手(合法手)の中からランダムに選択した手を打つ戦法(もはや戦法
	とは言えないですが)です。

	(3) 原始モンテカルロ探索
	 �@ そのとき打つことができる手(合法手)を求めます。
	 �A 各合法手を１手目として打った状態において、２手目以降は合法手の中からランダムに選択
	　した手を打つ戦法で終局まで行きます(プレイアウト)。その結果、先手の勝ちなら +1、後手
	　の勝ちなら -1、引分けなら 0 をその１手目に報酬として与えます。
	 �B �Aの操作を設定したプレイアウト回数だけ行い、累計報酬が最大の１手目を次の手にする
	　戦法です。

	(4) モンテカルロ木探索
	(参考:AlphaZero 深層学習 強化学習 探索 人工知能プログラミング実戦入門「布留川英一著」)
	　原始モンテカルロ探索を改善するやり方は種々考えられますが、ここでは次のようにしていま
	す。
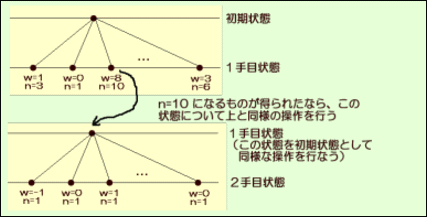
	 �@ 初期状態
	　　まず、１手目の合法手を打ったそれぞれの状態に対し、原始モンテカルロ探索で一回対局し
	　結果に応じて各手に報酬 w(=1,-1,0 のいずれか)を与えます。また各手の試行回数を n=1 と
	　します。

		

	 �A 選択
	　　各手の UCB1値=勝率+バイアス を次式で求めます。
		
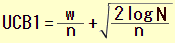	　ここで w=この手の累計報酬、n=この手の試行回数、および N=合法手すべて(この手も含む)
	　の試行回数の和、log は自然対数です。UCB1値が最大のものを次の手に選択します。そして
	　２手目以降は原始モンテカルロ探索を行い終局まで行き結果を出します。
	 �B 更新
	　　結果に応じて、この手の累計報酬と試行回数を更新します。この状態で、また�Aを行います。
	 �C 展開
	　　このような操作を何回か行なうと、試行回数が n=10 になるものが得られるので１手目を
	　この手に決めこの手を打った状態を作ります。さらに、この状態を初期状態として �@〜�Bの
	　操作を行い２手目を決めます。

		

	　　以下同様にして３手目、４手目、… 終局まで進み、この結果の報酬と試行回数を１手目に
	　付加します。これで１回目の対局が終わりで、プレイアウト回数=1 とします。
	 �D １回目の対局を終えた状態において、２手目以降の試行回数などのデータはすべて破棄しま
	　す。
	　　１手目の累計報酬、試行回数を用いて �@からの操作を行いプレイアウト回数=2 とします。
	 �E このようにして、定めたプレイアウト回数だけ対局を行い、その結果１手目の合法手の中で
	　試行回数最大の手(累計報酬最大の手ではない)を、１手目に打つ手として採用します。
	

	　結果についての感想
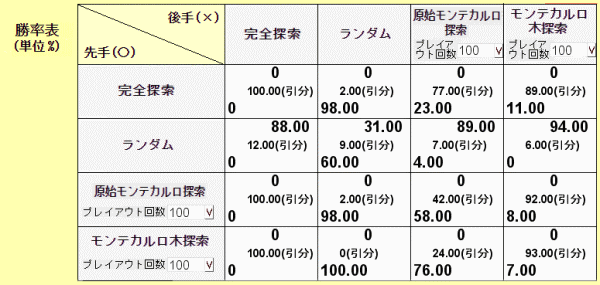
	　対局回数を100回として、先手、後手を種々の戦法で対局させた結果を一例として下図に示す。
	〇 先手後手とも完全探索であれば、100% 引分けになる。
	〇 先手が完全探索のとき先手が負けることはない。後手が完全探索のとき後手が負けることはない。
	〇 ランダムより明らかに原始モンテカルト探索やモンテカルト木探索の方が強い。しかし、モンテ
	　カルト木探索が原始モンテカルト探索より強いようには見えない。何かやり方がよくないのだろ
	　うか？ モンテカルト木探索のやり方を検討し改良することが今後の課題である。

		

　　　　　　　　　　　　　　　　お楽しみいただければ幸です。以上