> おもちゃ箱
迷路探索 (HTML版) 〇 迷路探索のシミュレーション実験を行います。 〇 手法、設定をいろいろ変えて試し比較してみてください。実験10番までできます。 詳細は下の 迷路探索について をご覧ください。 関連作品 迷路自動作成 |
|||
| Copyright(C) 2020-,YokahiYokatoki |
| 迷路探索 について (記：2020年8月17日、追記：2020年9月7日) | |
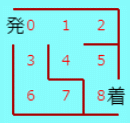
平面内の迷路で、マス数が n×n とする。n は３以上の任意の整数でよいが、ここでは、n=3, n=6 および n=10 のものを扱う。 n=3 のものを左図に示す。これは、布留川英一著「AlphaZero 深層学習・強化学習・探索 人口知能プログラミング実戦入門」 で扱われているものである。以下の説明は、この n=3 の迷路で行うが、任意の n の場合でも同様である。 発0 から 着8 まで通り抜ける最短路を見つける最も簡単で速く、しかも分かりやすい手法は、全探索である。 手法１ 全探索 各位置において、進むことができるすべての方向を試し最短路を見つける。力まかせの方法であるが、パソコンを用いれば瞬時に完了する。 このような迷路の解法は、全探索に勝るものはなくこれで充分である。 ところで、将棋や囲碁などのゲームにおいては最善の次手を見つけるのに全探索を行うことはできない。勝敗がつくまでの可能な手が天文学的な数存在するからである。このような場合に有効として用いられるのが、強化学習の手法である。 迷路の解法に、強化学習の手法として知られている方策勾配法を用いることは非効率的で、用いる必要はない。ただ、方策勾配法とはどういうものかを知るという目的のために、敢えてやってみよう。 手法２ 方策勾配法 (参考とした書籍は、布留川英一著「AlphaZero 深層学習・強化学習・探索 人口知能プログラミング実戦入門」など) ① 位置0～7 (位置8は目的地なので除く) において、行動(移動方向)は、上、右、下、左 の４通りある。これらの情報を、次のように 8行4列 の行列で表し、パラメータ行列 m とする。位置0 については、右および下方向に移動可能なので 位置0 について m の0行目 = [0, 1, 1, 0] (0:移動不可 1:移動可能) 以下同様に 位置1 について m の1行目 = [0, 1, 1, 1] 位置2 について m の2行目 = [0, 0, 0, 1] … 位置7 について m の7行目 = [0, 0, 0, 1] ② パラメータ行列 m を 方策行列 M に変換する。方策行列とは、位置 i にいるとき次の行動(どこに移動するか)を確率で表すもので、次のようにして作る。例えば、[0, a, b, 0] (a,b は 0 でない) のような行があるとする。要素 0 は 0 のままとし、0 でない要素については a → exp(a)/(exp(a)+exp(b)), b → exp(b)/(exp(a)+exp(b)) とする。すなわち、ソフトマックス関数を用いその行についての要素の和が 1 になるようにする。結果として次のようになる。 M の0行目 = [0, 0.5, 0.5, 0] M の1行目 = [0, 0.333…, 0.333…, 0.333…] M の2行目 = [0, 0, 0, 1] … M の7行目 = [0, 0, 0, 1] ③ 方策行列 M を ② で得たものを初期値として、位置0 から出発して 位置8 に辿り着くまで行動する。このときのステップ数を T とする。また N0[i][j]=位置i において、行動j (j は 上、右、下、左のいずれか) を取った回数 N1[i]=位置i において、(jも含めて)なんらかの行動を取った回数 (jは除いた方が正しいのか、自分で導出して確かめていないが、どちらでやっても最終的にはあまり関係しない？) とする。これらの情報を用いて、パラメータ行列 m を次式で更新する (いきなり方策行列 M を更新するのではない。M は確率を表すものなので、更新したパラメータ行列 m に対してソフトマックス関数を用いその行についての要素の和が 1 になるようにする)。(次式の導出については、ちっとした数学を用いればよさそうだが、私はまだ確認はしていない。暇なときに楽しんでみよう。) m[i][j] ← m[i][j]+η×(N0[i][j]-M[i][j]*N1[i])/T) (ηは学習率で η=0.1 とする) さらに、このパラメータ行列 m についてソフトマックス関数を用い、更新した方策行列 M を求める。これを 学習１回分(1 エピソード)とする。 以下 ③ を繰り返すこと(学習サイクル)によって方策行列 M を更新し、変化量が閾値(しきいち)以下になったら完了である。 後は得られた方策行列 M を用いて移動する。すなわち、M の0行目 の要素のうち最大の確率の方向に移動(例えば 1列目の要素が最大だったら右に移動する)。以下同様に、位置 i に居るときは、M の i行目 の要素のうち最大の確率の方向に移動する。その結果、位置8 に辿り着いたら探索成功である。 方策勾配法は以上である。これはこれでなんとかうまく迷路の最短路を見つけることはできる。ただし、もし目的地までの経路が何通りかあるような迷路の場合、この方法で学習が進めばより最短路に近づくかも知れないが、最短路が得られる保証はないのでないか、と思う。 本来、このような迷路の探索に方策勾配法の手法を用いることは非効率的である。なぜなら、位置8 に辿り着いたら１回の学習として方策行列 M を更新、これを繰り返すのであるが、もう目的地までの経路は得られたのだからそれでいいではないか。それが最短路ではないかも知れないが、大体この手法は最短路を見つけるものではないので、１回の学習で終了してもよいと思うのである。もっともそれでは方策勾配法という手法にはならないことになってしまうので、これは目をつむるしかない。 ところで、一度来た位置に再度来た場合にはそこまでの経路情報は無駄なので削除してもいいのではないか。そうすればより速やかに目的地までの経路が得られるだろう。（注：「８割は２割の労力によって成される」 というパレートの法則を信じ、さらに「2.5%の労力しか使わず６割の成果で満足する」 ことを信条とする私の感想なので、このまま私の言うことを本気にしないで自ら思考を巡らしていただくことを願う。） ということで、次の手法もやってみよう。 手法３ 方策勾配法_改 手法２の方策勾配法において、一度来た位置に再度来た場合にはそこまでの経路情報は無かったものとして学習するようにする。 手法２の方策勾配法より、速やかに結果が得られる。無駄な経路情報を用いないので、変化量が閾値以下になるまでの学習回数は何度やっても同じ回数になるのは当然であるが、所要時間は(平均すると)短縮される。 方策勾配法は、位置0 から出発して 位置8 に辿り着くまで(１エピソード）毎に方策行列 M を更新する手法である。それに対して、１行動をとる度にパラメータ（行動価値関数 や 状態価値関数）を更新し最適化する価値反復法と呼ばれる手法がある。布留川英一著「AlphaZero 深層学習・強化学習・探索 人口知能プログラミング実戦入門」では、行動価値関数を用いた Sarsa と Q学習 についての解説があるので、これに従ってやってみた。 手法４ Sarsa ① パラメータ行列 m を用意する。これは手法２のものと同じである。 ② パラメータ行列 m を 方策行列 M に変換する。これも手法２で説明したように、各行についての要素の和が 1 になるようしたものでであるが、ソフトマックス関数を用いる必要はなく単なる割合計算でよい。M は更新することはない。 ③ 行動価値関数 Q を 用意する。初期値は、移動可能な方向は 0より大きく1より小さい範囲の乱数で与え、移動不可の方向は 0 とする。 さて、t=0 ステップから始めるわけであるが、一般的に述べると次のようになる。t ステップの行動 a[t] (上、右、下、左 のいずれかの移動)を終えて s[t] のマス位置に居るとする。次の (t+1) ステップ目 の行動 a[t+1] は次のようにして決める。 ④ 乱数を発生させ、確率 ε 以下なら ②の行列 M の確率で行動し、ε より大きいなら ③の行列 Q において現在位置の行の要素の内で最も大きい値の方向に移動する（ε-greedy 法。学習１回目では ε=0.5 とするが、学習回数が増す度に ε*0.5 を改めて ε 値とする）。その結果として s[t+1] を得る。 ⑤ 行動価値関数 Q の Q[s[t],a[t]] の要素を次の式で更新する。 s[t+1]=8 のとき、R=1 として Q[s[t],a[t]]=Q[s[t],a[t]]+eta*(R-Q[s[t],a[t]]) s[t+1]<8 のとき、R=0 として Q[s[t],a[t]]=Q[s[t],a[t]]+eta*(R+gamma*Q[s[t+1],a[t+1]]-Q[s[t],a[t]]) ここで、eta は学習係数 で eta=0.1 とし、gamma は時間割引率 で gamma=0.9 とした。R は 即時報酬である。 そして、 s[t+1]=8 なら、１回分の学習終了。次の学習として ① から繰り返す。ただし、③ は行わず今までの学習で得たものを継承して用いる。 s[t+1]<8 なら、次のステップに進み ④ から繰り返す。 念のため30回までの学習を行ってみたが、それ以下の時点で収束した結果が得られるようだ。 手法５ Q学習 Sarsa と異なるのは、⑤での 行動価値関数 Q の更新式のみで、他は同じである。 ⑤ 行動価値関数 Q の Q[s[t],a[t]] の要素を次の式で更新する。eta=0.1、gamma=0.9 とする。 s[t+1]=8 のとき、R=1 として Q[s[t],a[t]]=Q[s[t],a[t]]+eta*(R-Q[s[t],a[t]]) s[t+1]<8 のとき、R=0 として Q[s[t],a[t]]=Q[s[t],a[t]] +eta*(R+gamma*(Qのs[t+1]行の要素の内の最大値)-Q[s[t],a[t]]) Sarsa、Q学習 において同じような結果を得る。変化量が閾値以下になるまで学習を行うようにはしていない（50回までの学習で打ち切り）ので、所要時間の方策勾配法との比較はできないが、短時間で完了はする。行動価値関数 Q の更新式についてじっくり考えてみることが最も重要なことで、その意図することが分かってくれば、Q の更新の他のやり方や改良案が生まれると思われるが、これ以上はのめり込まない。 いろいろ実験をして比較してみると楽しめる。ただ、扱った迷路が簡単すぎるせいか、各手法の実力が実感し難いように思う。と言っても、n をあまり大きくすると手法１の全探索以外の手法では時間がかかる。 次のような n=6 と n=10 の迷路を作ったので、これらの迷路でも、いろいろ実験をし比較してみると楽しめる。   ∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞ |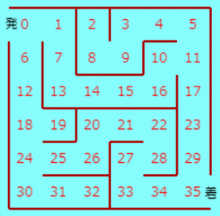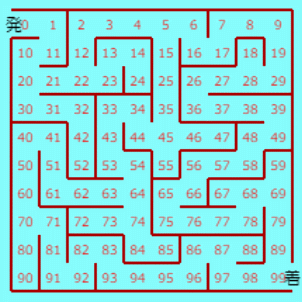
|
| Copyright(C) 2020-,YokahiYokatoki |