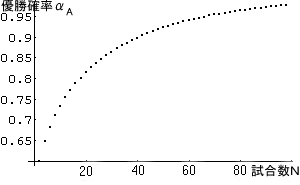
今年の日本シリーズはダイエーの２連勝…まではよかったが、その後４連勝した巨人が日本一になってしまった。福岡に住む私としてはダイエーを応援していたので残念である（ほんとうは私は出身が広島県なので子供の頃からの大のカープファンである）。ところで、ほんとうに巨人がダイエーより強いのか？ 早い話がもし、日本シリーズは１試合のみで決着を付ける、ということだったならばダイエーが日本一ではないか。あるいは、先に２勝したら優勝、ということでもダイエーが日本一ではないか。なぜ先に４勝しなくてならないのだ。それなら先に５勝したら優勝ということだったらもしかしてダイエーが逆転していたかもしれないじゃあないか。とやや感情的に屁理屈を並べてみても、ただ見苦しいだけの負け惜しみでしかないだろうな。ここはひとつ潔(いさぎ)よく…、うーん、潔わるくせめて冷静に考えてみよう。
　巨人とダイエー戦はひとまず置いといて、ここでは客観的に冷静沈着に考えてみよう。まず、ＡとＢの２チームの内のどちらが真に強いのか、はどうして決めるのかをはっきりしておかなくてはなるまい。Ｎ(Ｎ＝１,２,３,…) 試合して、Ａがａ回勝ち、Ｂがｂ回勝ったとすると(ただし、ａ＋ｂ＝Ｎ)、Ａの勝つ確率は Ｐ_Ａ＝ａ／Ｎ、Ｂの勝つ確率は Ｐ_Ｂ＝ｂ／Ｎ＝１−Ｐ_Ａ である。Ｐ_Ａ＞Ｐ_Ｂ のときＡがＢより強い、ということにしよう。問題は試合数Ｎをいくつにすべきかである。ちなみに日本シリーズは先に４勝した方が優勝ということなので、Ｎ＝７ にしていることなる。しかしながら、Ｎはできるだけ大きいほうがよく、理論的にはＮ→ ∞ であるべきである。よって、
　　［定義］ＡがＢより真に強いとは Ｐ_Ａ＞Ｐ_Ｂ (Ｎ→ ∞)である、また逆に、Ｐ_Ａ＞Ｐ_Ｂ (Ｎ→ ∞) のとき ＡがＢより真に強い。
のように決める。待てよ。実際には無限回の試合をやることはできない。そうか。そこに我々の疑問と不満が残るわけだ。つまり、何試合かをしただけで日本一を決めるというけれど、それはただ優勝チームを決めるということであって、日本一強いチームを決めることではないのだ。
　では、日本シリーズで優勝したチームが負けたチームより強い、と言った場合の誤った判断の確率を考えてみることにしよう。いま無限回戦ったとして、勝つ確率Ｐ_ＡのチームＡと、Ｐ_ＢのチームＢとがあって、Ｐ_Ａ＞Ｐ_Ｂと仮定しよう。さて、
　［ルール］この２チームの内先にｎ勝した方が優勝とする。すなわち 試合数Ｎ＝２ｎ−１ で決着をつける。(実際には、どちらかのチームが先にｎ勝したらそこで終了である。)
としよう。このとき Ａ が優勝する確率は２項定理あたりを用いて、
　α_Ａ＝Ｃ(Ｎ,０)Ｐ_Ａ^Ｎ＋Ｃ(Ｎ,１)Ｐ_Ａ^(Ｎ−１)Ｐ_Ｂ＋Ｃ(Ｎ,２)Ｐ_Ａ^(Ｎ−２)Ｐ_Ｂ^２+ … ＋Ｃ(Ｎ,ｎ−１)Ｐ_Ａ^{(Ｎ−ｎ＋１)}Ｐ_Ｂ^(ｎ−１)
であることが示せる。ここで、Ｃ(Ｎ,ｒ)はＮ個の異なる物からｒ個選ぶ場合の数である。
　Ｎ(Ｎ＝１,３,５,…) の値に対して、α_Ａがどのような値をとるかを、例として Ｐ_Ａ＝０.６ としたときの計算結果をグラフに示した。Ｐ_Ａ＞０.５ なのでＮが大きくなればなるほどＡが優勝する確率α_Ａは１に近づくことは言うまでもない。

　　Ｐ_Ａ＝０.６ としたときのＮ試合でのＡの優勝確率

Ｎ	αＡ
１	０．６００
３	０．６４８
５	０．６８３
７	０．７１０
９	０．７３３
１１	０．７５３
：	：
９７	０．９７７
：	：

　 さて日本シリーズは試合数Ｎ＝７である。この例の場合だと Ｎ＝７のときα_Ａ＝０.７１０ なので、
　巨人が優勝したので巨人が強い、という判断が間違っていない確率は ０.７１０
でしかない。逆に
　巨人が優勝したけれどダイエーが強い、と判断しても間違っていない確率は ０.２９０
もある、ということになる。この数値で、胸を張って「それでもやっぱりダイエーの方が強いもんね。」と言っていいものかどうかは謙虚な私には自信がない。ただ、Ｐ_Ａ＝０.６ の値が妥当なものなのかはわからないし、大体Ｐ_Ａの値は誰にも永遠にわからないのだから...結局我らのチームを信じるものが救われる？

　二項定理：(ｐ＋ｑ)^Ｎ＝Ｃ(Ｎ,０)ｐ^Ｎ＋Ｃ(Ｎ,１)ｐ^(Ｎ−１)ｑ＋Ｃ(Ｎ,２)ｐ^(Ｎ−２)ｑ^２+ … ＋Ｃ(Ｎ,Ｎ)ｑ^Ｎ
　右辺の展開式における係数Ｃ(Ｎ,ｒ)＝Ｎ！/{(Ｎ−ｒ)！ｒ！} (ｒ＝０,１,２,…,Ｎ) を二項係数という。