 | 『図のようにケーキを2回包丁を使って4つに切った。ところが8人家族である。あと1回だけしか包丁を使えないとしたら、あなたはどうしますか?』 |
という問題がある。 これを数学の授業中に話したら、即座に「横に包丁を入れる」というだれでも思いつく 意見が出た。他に無いか? と言うと、さすが自由な発想を良しとする(?)本校の学生諸君からは、その 他様々な意見が出た。もちろん4つを縦に積み上げて上から切るというような方法も出た (これではせっかくのケーキがグチャグチャ になると思うが、数学的?には間違いではないだろう)。 一人女子学生がニヤニヤしていたので、その学生に意見を 求めると、 「4人を並べておいて包丁でたたっ切る」 との発言である。参った。リストラの発想か。身に迫るものがあるぞ。 いつものように夜帰宅して鞄を置くやいなや、小学生の娘にいきなり丁寧に質問された。 「もしお父様が死んだら、 世界はどのように変わると思いますか?」 「そうだなあ、私のような重要人物が亡くなると、世界は大きく変わるだろうなあ。」 すると、娘は 「ちがいます。もしお父様が死んだら、世界の人口が1人減ります。」 そりゃなぞなぞか? 丁寧な言葉使いはいいが、 お父様はひどく傷付いておるぞ。頭は薄い、いや柔らかいはずの私であるが、このところやられっぱなしである。 だれが何と言おうと、私は無事元気に長生きすることに決めている。 ところで、職場では毎年10月になると集団検診が実施される。40歳を過ぎた人は、 胃通し(バリウムを飲んでX線写真を撮る)をしなくてはならないが、これがなにより苦痛である。もっとも、癌は遺伝的要素が大きいそうであるから、私は受けた方が いいに決まっている。親父は44歳にして胃癌で命を落としたし、6人兄弟のうち2人の兄は既に胃を切り取った。 (昔、兄が大阪の会社での就職面接のとき、「あなたのお父さんは、いがんで(ゆがんで) 亡くなられたのですか?」 と問われ、「いいえ、まっすぐになって死にました」 と答えて面接官に受けた。) 私も検診をするたんびに、 要精密検査の通知をいただく。初めての年はあわてて精密検査を受けたが幸い異常なし、その後は受けていない。これでは何のために 胃通しを受けているのか...我ながら異常である。うちの婆ちゃん(家内の母)にいたっては、検査で癌であるとわかったら怖いので始めから 検査を受けない。 要精密検査の知らせをもらっても、それを無視している人がかなりいるのではないだろうか。そのような人を安心させることに なるのかどうかは判らないが、田中義厚著「確率の人生学」(青春出版社) という本に書かれていたことを、胃癌検診の場合に当てはめてみたら次のような結論を得たので紹介しよう (これはあくまでお遊びです)。 まず、胃癌検診の信頼度はどれ位のものなのかは知らないが、仮に98%の正確さであるとしよう。その意味は、 ● 本当に胃癌になっている人のうち、98%の人は要精密検査必要とされ、残り2%の人は異常なしと診断される。 ● 本当は胃癌ではない人のうち、98%の人は異常なしとされるが、残り2%の人は要精密検査必要と診断される。 ということにしてみよう。 さて、日本において40歳以上で胃癌になっている人の割合がこれまたどれ位のものかは知らないが、仮に0.01%であるとしよう。 40歳以上の人口を1億人とすると1万人の人が胃癌である。1億人の人全員がこの検診を受けたとすると、何人の人が 要精密検査であると診断されるかというと、 ●胃癌である1万人の内98%の9800人が要精密検査であると診断される。 ●本当は胃癌でない9999万人の内2%の199万9800人が要精密検査であると診断される。 よって、この検診で9800+1999800=200万9600人が要精密検査であると診断される。この内本当に胃癌の人は9800人である。 すなわち約201万人が要精密検査と診断されるが、そのうち本当に胃癌の人は9800人でしかない、ということである。 98%の正確さの胃癌検診で引っかかったからといっても、9800÷2009600×100=0.49%、すなわち、1000人の内うち精々5人 が本当に胃癌であるにすぎない。 ということになるのである。 この確率は考えようによってはかなり大きいとも思えるが、お年玉年賀ハガキにもめったに当たったことのない私には、すこし安心できる結論ではある。 ただし、上の議論にはいくつかの無責任な仮定が含まれていることをお忘れなく。無事元気に長生きするためには、やはり自分の責任で精密検査は受けた方が.....。 (2001. 8.26)
|
|
もし胃癌検診の信頼度が99%であるなら、要精密検査1000人の内うち約10人が本当に胃癌である。 もし胃癌検診の信頼度が99.9%であるなら、要精密検査1000人の内うち約91人が本当に胃癌である。 もし胃癌検診の信頼度が99.99%であるなら、要精密検査1000人の内うち約500人が本当に胃癌である。 もし胃癌検診の信頼度が99.999%であるなら、要精密検査1000人の内うち約910人が本当に胃癌である。 うわあ〜、もういいです。 |
(しつこく)
もし胃癌検診の信頼度が χ %であるなら、要精密検査の通知をもらった人が本当に胃癌である確率 y は、 χ y=――――――― 999900-9998χ また、精密検査は必要なしの通知をもらった人が本当は胃癌である確率 z は 100−χ z=―――――― 100+9998χ 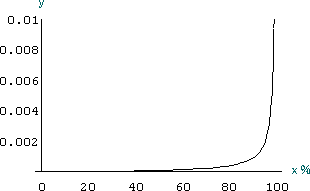 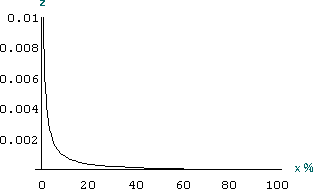
|
**********************************************************************************
Copyright(C) Yokahiyokatoki
 > 『数学的思考(?)エッセイ』 の試み
> 『数学的思考(?)エッセイ』 の試み