寝てる間も増えてほしい、といっても髪の毛の話ではない。現在の郵便局での通常貯金の年利率は0.02%だそうだ。つまり、100万円を1年間預けておいてもわずか200円の利息しか付かない(計算間違いではない!)。1億円ならどうだ。むろん預ける金は無いからなにも心配することは無いのだが、せめて計算だけでもしてみよう。2万円だ。これを長期定期にしてもやっと7万円程度。預ける金をほとんど持たぬ小生は、悔しい思いをしなくてよいことをせめてもの幸せだと思う(くうっ…)。 ところで、次のような疑問がわいてきた。貯金や預金の利息はたいてい年利率で決めてあるが、いつでも解約できる通常貯金などは日割で利息を計算してくれるはずである(たぶん)。いくら親切な郵便局や銀行でも、解約した時間や分、秒によっていちいち利息を計算してくれるところはないと思うが、だいたい預けたお金は我々が寝ている間でも時々刻々連続的に利息が付くようになっているのだろうか、ということが気になった。もしそうなら "瞬間利率" はどのようになるのだろうか? 気になる。預ける金も持たないのにこんなことを気にしても時間の無駄だと思うような気もするが、気になるものはしかたがない。 さて、元金a円を年利率r%で預けたときの元利合計A円は(複利として) 1年後: A=a+a×r/100=a(1+r/100) 2年後: A=a(1+r/100)+a(1+r/100)×r/100=a(1+r/100)2 : y年後: A=a(1+r/100)y で与えられる。 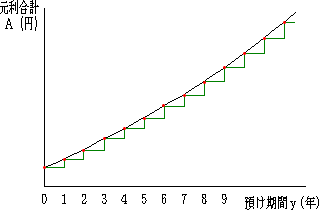 日割で利息を計算してくれるなら、上式でy年を日の単位に変えるために、y=d/365 として d日後: A=a(1+r/100)d/365 とする。この式を変形すると d日後: A=a[(1+r/100)1/365]d=a[1+100{(1+r/100)1/365−1}/100]d となるので、日利率 rd は rd=100[(1+r/100)1/365−1] で与えられることがわかる。これは近似的には、rd≒r/365% である。ちなみに、r=0.02% のとき、rd=0.0000548%であり、1億円に対して、利息は1日54円(≒2万円/365)である。 さらに、預けてからの時間を秒ではかって秒割で利息を計算してくれるなら、同様にして t秒後: A=a(1+r/100)t/(365×24×3600) =a[1+100{(1+r/100)1/(365×24×3600)−1}/100]t となるので、秒利率 rs は rs=100[(1+r/100)1/(365×24×3600)−1] この値は、とてつもなく0に近い(もちろん0ではない)。 一般に、元金a円を年利率 r%で預け、利息の計算をk年 (0<k≦1) 単位でやってくれるとしよう。y年をk年単位に変えるために、y=kt として t(k年単位)後: A=a(1+r/100)kt=a[1+100{(1+r/100)k−1}/100]t これより、k年当たりの利率 rk は rk=100[(1+r/100)k−1] となる。k→0 の極限で、rk→0 となり、瞬間利率なるものは意味をなさない。利率 rkの定義は、ある期間kにおける現在の元金に対する増加の割合である。したがって、rk→0 (k→0) となることは冷静になってみると当然であった。 "瞬間の率" なるものを考えるためには、ある期間kに対する増加高を考えるしかない。そこで、A=a(1+r/100)y において、yは本来離散的な値しかとらない変数であるが、正の実数をとり得るとしてyで微分して dA/dy=Alog(1+r/100) を得る。これは瞬間の増加率であるがA自身に比例するので、単位金額当たりの瞬間の増加率をR%として R/100=log(1+r/100) を得る。利率rが低いと、年利率は瞬間の増加率R%とほぼ等しいことになる(下表参照)。
(2001.11.1)
|
|||||||||||||
都筑卓司著「なっとくする統計力学」(講談社)P.74 と、上野健爾著「数学と総合学習」数学セミナー2000年8月号 P.58(日本評論社)には、次のような議論がある。 年利率R%で元金a円を預けたときの1年後の元利合計A円は、A=a(1+R/100) で与えられるが、半年ごとに利率がR/2%の複利とすると1年後の元利合計は、A=a[1+R/(2×100)]2となる。さらに、4か月ごとの利率がR/3%の複利とすると1年後の元利合計は、A=a[1+R/(3×100)]3となる。一般に、1/n年ごとの利率がR/n%の複利とすると1年後の元利合計は、A=a[1+R/(n×100)]nとなる。n→∞ の極限をとると Aはいくらになるか? 答えは、A=aeR/100 である。 A=aeR/100=a(1+r/100) とおくと、R/100=log(1+r/100)。上で求めた関係式は結局これと同じものだった。 |
**********************************************************************************
Copyright(C) Yokahiyokatoki
 > 『数学的思考(?)エッセイ』 の試み
> 『数学的思考(?)エッセイ』 の試み