最近は電卓やパソコンですぐに求められるから、わざわざ憶えておく必要もないのであるが、常用対数の log102 と log103 の値くらいは、理系畑の人は憶えているとなにかと便利なものなのである。 例えば、230 が何桁の数になるかは、log102≒0.3010 を知っていれば、「0.3010×30=9.030 より10桁の数になる」 ということが直ちに分るのである。
この log102≒0.3010 の値は、また別の意味でも重要な値であることは、残念ながら世間ではまだ知られていない。すなわち、月日が逆順になっているが、私の誕生日が10月30日なのである。(シツレイシマシタ) log102≒0.3010 が私の誕生日を予言したものであるとするなら、log103 は私の命日を予言したものに違いないと考えられるが、これがなんと log103≒0.4771 (シナナイ)、すなわち私は不死身なのである。(再度シツレイシマシタ) 冗談はこれくらいにして、私もついに50歳に突入してしまった。このところ1年が経つのがとてつもなく速くなったと感じるのは、私が歳を取った証拠であろう。歳を取るにつれて時の経つのが速く感じられる理由にはいろいろあるのであろうが、その一つとして次のことが言われている。例えば10歳の子供にとっての1年間は今まで生きてきた時間の10%であるが、50歳の人にとっての1年間は2%でしかない、だからであるというのである。このような理屈に科学的根拠があるのかどうかは知らないが、もっともらしい理由ではある。 そこで、この理屈が正しいとしたらいったいどういうことになるのだろう、と考えてみたくなった。つまり、カレンダーや時計のような日時を確かめる手段をいっさい持たなかったとしたら、自分が生まれてから現在まで自分の生きたと感じる年月はいったいどれだけのものか? ということである。 まず時間の単位を1年としよう。そして、実際に生きた年数を "実際年"、我々の感じる年数を "感受年" と呼ぶことにして区別しよう。もちろん 1感受年≦1実際年 であるが、1感受年が1実際年の何%になるかは、"その人のその日時点での生きた年数による" ということである。さて1感受年の基準を決めておかなくてはならないが、生まれて最初の本当の1年間はやはり1年間と感じることにしよう。 (1) モデル−1
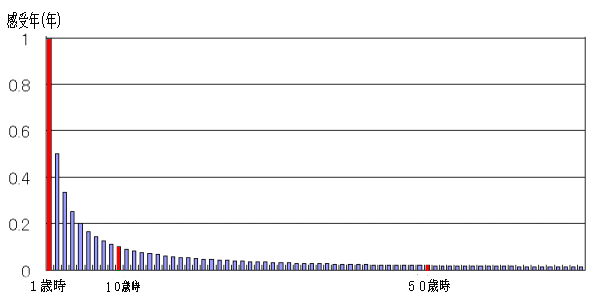 図1. (n−1)〜n年までの実際年1年=感受年1/n年 とした場合
さて、実際年齢がn歳の人にとっての感受年齢 Yは何歳であるかを計算してみよう。これは
Y=1+1/2+1/3+…+1/n のように与えられる。これで計算すると、例えば実際年齢で70歳まで生きたとしても、感受年齢はわずか5歳にもならないということになる (図2)。これはちょっといくらなんでも認め難い。 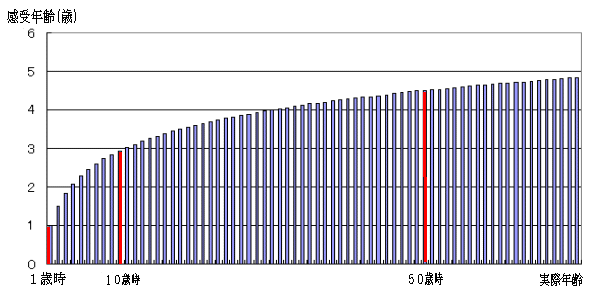 図2. (n−1)〜n年までの実際年1年=感受年1/n年 とした場合の感受年齢
我々の命が誕生するのは誕生日ではなく、その前に母親の胎内で十月十日過ごしていたことを忘れていたが、それを考慮してもあまり関係なさそうだ。また、ものごころがついてからの1年を感受年1年としたとしても、大して影響はなさそうだ。考え直そう。
(2) モデル−2 歳を取るにつれて時の経つのが速く感じられる理由として、初めて眼にしたり耳にしたりする量、すなわち新しく体験する量が日増しに減ってくるからだという説がある。確かに、生きるということは新しい時間を過ごすということであるから、体験の量が年齢であるということができるかもしれない。 この世での我々が体験できる量はほぼ一定N0であるとしよう。自分が今までに体験した量をYとすると、まだ体験していない量は (N0−Y) であり、自分が新しく体験する量の増加率は、このまだ体験していない量 (N0−Y) に比例するであろう。すなわち、生まれてからの時間をnとして dY/dn=k(N0−Y) (k は正の比例定数) これを解くと Y=N0(1−e−kn) となる。いま、N0=A/(1−e−k)、e−k=r (A、rは定数で 0<r<1) とおくと次のようになる。 Y=A(1−rn)/(1−r)=A(1+r+r2+r3+…+rn−1)
上式は、nが連続的な時間として導いたものであるが、n=1,2,3,… 年 と考えると次のことを意味する。すなわち、生まれて最初の1年はやはり1年と感じるが、1〜2歳までの1年間は r年と感じ、2〜3歳までの1年間は r2年と感じ、3〜4歳までの1年間は r3年と感じ、… というようにどんどん短く感じる。すなわち、生きた実際年が (n−1)〜n年までの1年を我々は rn−1年と感じるということである。 (図3) 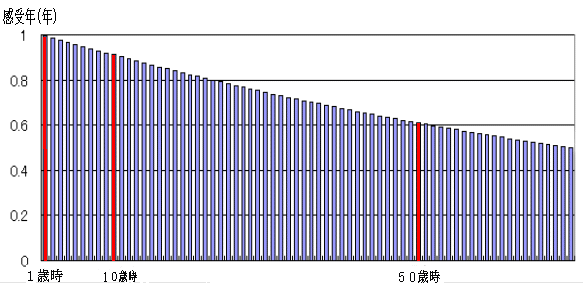 図3. (n−1)〜n年までの実際年1年=感受年 rn−1年 (r=0.99)とした場合 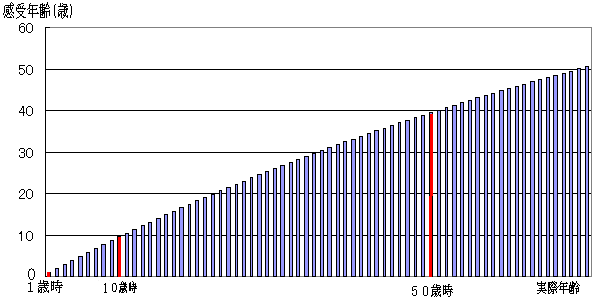 図4. (n−1)〜n年までの実際年1年=感受年 rn−1年 (r=0.99)とした場合の感受年齢
モデル−2 の方は、我々が感じている時間をよく表しているように思うがどうであろうか。ただし、例として r=0.99 としたものを示したが、人によっては r が限りなく1に近い人もいるだろうし、あるいは r=0.8 ぐらいの人もいるかも知れない。r の値は、その人が如何に新しいことに挑戦し続けた充実した人生であるかどうかを表す指標ということができるかもしれない。あなたのr指標はいくつだろうか?
(2001.11. 6)
|
|||||||||||||||||||||||||||||||||||||||||||||
数列 A、Ar、Ar2、Ar3、… を、初項A、公比 r の等比数列という。第n項目は、Arn−1 である。また、初項から第n項までの和 Y=A+Ar+Ar2+Ar3+ … +Arn−1 は、Y=A(1−rn)/(1−r) で与えられる。
|
**********************************************************************************
Copyright(C) Yokahiyokatoki
 > 『数学的思考(?)エッセイ』 の試み
> 『数学的思考(?)エッセイ』 の試み