私の愛読書の1つに、中谷宇吉郎著 「科学の方法」 がある。 何回か読んだが、その度に感銘を受ける。その中に次のような話がある。(以下要約) 「地球の形はどんな形ですか?」 と尋ねると 、小学生は 「円い」 と答え、中学生は 「楕円体 (南北に少し縮んでいる)」 と答え、大学生なら 「擬似楕円体」 であると答える。ところが地球物理学者にいわせると 「地球の形はそれらのいずれでもなく、地球形」 であると答えるのだそうである。 では、その形を紙に描けといわれると、結局コンパスで円を描くより仕方がない。 世界最高峰の高さや海溝の深さも精々10km。 赤道面内の半径より南北の半径が短いといっても 約22kmだけ。 鉛筆の線の幅は約44kmにもなるので、地球の歪や地表面の凸凹はすべて線の幅に入ってしまうのである。擬似楕円体などというものはもっと細かい話である。だから、小学生の答えが一番適切なものなのである。 話変わって、授業で教室に行くと、なぜか教卓にトイレットペーパーが置いてあることがある。学生がトイレから持ってきたものであろうが、このような紐の代わりになるものをみると、マジックをやって見せたくなる性分である。実際、授業が一区切りついたところで息抜きに、「じゃあ、マジックをやってみるから騙されないように、マあジックり見ておけよ。」 とかなんとか言いながらやってみせると、学生が私を尊敬した目で見てくれるのがわかる。これには複雑な心境である。「おいおい、どうせなら数学の方で尊敬してくれ。」 そこで、今日はこれを教材に数学でもやってみるか。  「このトイレットペーパーのおおよその長さを、計算で求める方法を述べよ。ただし、半径は a、芯の部分の半径は b で、ペーパーの厚さは d であるとする。」 まず、何回巻かれているかを計算すると、巻数 n=(a−b)/d である。トイレットペーパーの長さをLとする。 [方法1] n回巻かれているが、1巻きの長さは巻かれている位置によって異なるので、最大半径aと最小半径bの中間(平均)値をとって、2 L=(a+b) =(a+b)(a−b) [方法2] ペーパーが巻かれている部分の断面積を計算すると、 =(a+b)(a−b) (a+b)(a−b) これより、 L=(a+b)(a−b) [方法3] 巻かれている半径は、内側からb、b+d、b+2d、… のようにdだけづつ増える。よって 1番内側の1巻きの長さ=2 内側から2番目の1巻きの長さ=2 内側から3番目の1巻きの長さ=2 : 一番外側、すなわち n番目の1巻きの長さ=2 これらの総和がトイレットペーパーの長さLだから L=2 =2 =(2b+nd)n =(a+b)(a−b) [方法4] ペーパーが渦巻状に巻かれているとする。その方程式は極座標表示で 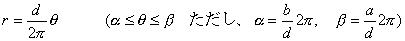 で与えられる。曲線の長さLは次の積分で与えられる。 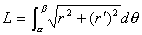 したがって、 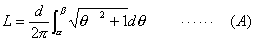 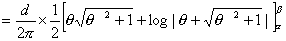 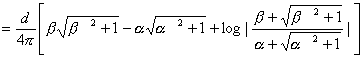 となる。[ ] 内の第3項目は第1、2項目に比べて微小だから無視できる。さらに、 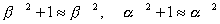 としてよいので としてよいので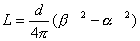 =(a+b)(a−b) となる。 あるいは、どうせ近似するなら上の(A)式以下、 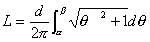 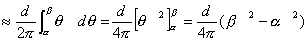 とした方がはやいか。 いずれの方法でも結局、同じことを同じように計算しているのだから同じ結果になるのは当たりまえである。 方法1が小学生、方法2が中学生、方法3が高校生、そして方法4が大学生の解法だとしたら、やっぱり小学生の解法が一番優れていて、「地球の形」の話が思い起こされる。何につけても小学校の勉強に本質が含まれている。 (2002. 1.19) [*このトイレットペーパーの長さを求める話は、岡部恒治著「考える力をつける数学の本」にヒントを得た。] |
**********************************************************************************
Copyright(C) Yokahiyokatoki
 > 『数学的思考(?)エッセイ』 の試み
> 『数学的思考(?)エッセイ』 の試み