夕食時、ケチャップのかかった物を箸でつまんで自分の皿にとっているとき、つい手がすべって落っことしてしまった。こともあろうに落ちたところが今日の晩酌の酒の中である。あれー、酒にケチャップが...　『やばいなぁ 』　と内心思いながらも、「こういう思わぬことから、新しい飲み物や料理なんかができるんだよねー。（一口飲んで）… おお、意外といける。」 といってみる。　「よかったね」 と娘らは、そっけない。（う〜うまいわけない〜）
　それはともかく、新しいアイデアは机上で論理的に考えても、なかなか沸いてくるものではない。実験のやり方を間違えたために、それが却って思いもよらぬ面白い結果をもたらし新しい発見につながった、ということはよくあることだ。特に学生は、ときにトンデモないことをしでかすこともあるが、だからこそおもしろい｡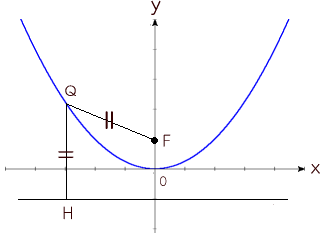

　さて、放物線は　「定点(焦点)と定直線(準線)からの距離が等しい点の軌跡」　として定義される（左図参照）。学生にこのことを身をもって(？)感じてもらうのによい方法がある。「紙を折って放物線を描き出す」　というものである。

　１枚の長方形の紙を用意する。まず、縦に２つに折り、中心に折り目を付け、その中心線上の適当な位置に点Fを付ける。
　次に、紙の下辺ＡＢ上の任意の点が点Ｆに来るように折って、折り目を付けて開く。次に、下辺ＡＢ上の点として、先の点から少しずれた点を選び、その点が点Ｆに来るように折って、折り目を付けて開く。このようなことを、下辺ＡＢ上の点で万遍なく繰り返してやる。

　そうすると、直線の折り目がいくつかできるが、これらの直線群に接している１つの曲線が見えてくる(包絡線という)。この曲線が点Fを焦点、下辺ＡＢを準線とする放物線である。


　学生に紙を配り上図のやり方を説明し、ではやってみて下さい、といって見て回っていると、たぶん説明をよく聞いていなかったのであろう学生が、おかしなことをしている。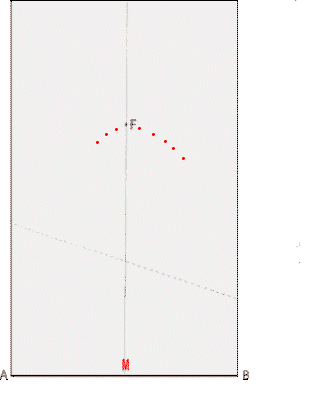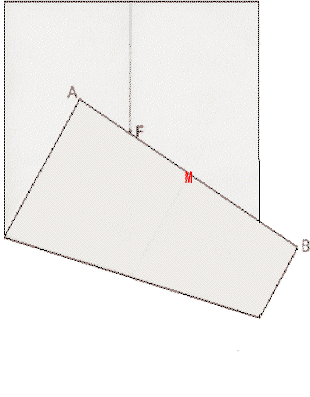

　下辺ＡＢを点Ｆに合わせて折るまではよいのであるが、そのときＡＢの中点Ｍが来た所に印を付けているのである。

　「おいおい、そうじゃあないよ」　と言ったものの、その学生のやり方でもヒョッとしたら放物線が描けるのかな、と疑問？？？ 　授業が終わって、さっそく点Ｍの描く軌跡の方程式を作ってみたら次のようになった。
　　16ｐ²ｘ²[ｘ²+(ｙ−ｐ)²]＝{２ｐｘ²＋２ｐｙ²−２ｐ³−(ｙ＋ｐ)[ｘ²+(ｙ−ｐ)²]}²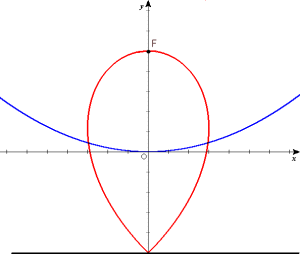

　折り紙でできる範囲では、連珠形のようなものができるが、連珠形ではない。


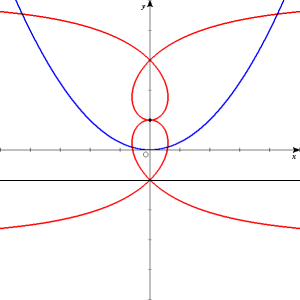　もっと広い区間でグラフを描かせると、おもしろい曲線になる。これは何という曲線だ？ 特異点を求める問題としてよく出てくるもののようだ。

　その他、いろいろな所に点を付けてみるともっとおもしろそうな曲線が得られそうだ｡

　思わぬ失敗から新しい思いつきをすることを、今後は密かに　「サケチャップ効果」 と呼ぶことにしよう。 「サケチャップ効果」 をもたらしてくれる学生がクラスに少なからずいることが数学の授業を楽しくする。