|
「天は人の上に人を造らず人の下に人を造らずと云へり」 有名な、福沢諭吉の 「学問のすゝめ」 の巻頭文であるが、要は 「人は皆生まれたときは
平等である」 と言っているのである。直接には言わないで、上記のように言うところに趣きがあり格調高く聞こえ、また心に残る所以である。
私も、この手法で何か名言でも残したい、と考えたが、悲しいかな教養の無さは致しかたが無く、格調ある名文が浮かぶわけがない。それは早々に見切りを付けて、名文ならぬ迷文を作った。 「およそ人生は、無駄より大、無駄未満である」 まあ、生きていくことに価値の上下を付けてもしようがない、というほどの気持ちである。ところで、今日話題にしたいことは、迷文のあまり意味の無い内容のことではなく、この苦し紛れ (?) の表現法は数学的である、ということについてである。 θ を限りなく 0 に近づけると、sin θ の値は 0 に近づく。このことを、 sin θ → 0 (θ → 0) と書く。 では、θ を限りなく 0 に近づけるとき、 sin θ/ θ はどんな値に近づくか? 分子は 0 に近づくが、同時に分母も 0 に近づくので、このままでは何ともわからない。 ところが、次のように考えればどんな値に近づくのかがわかるのである。 ここでは証明は示さないが、 cos θ < sin θ/ θ < 1 (-π/2 < θ < 0、0 < θ < π/2) が成り立つことが知られている。 cos θ → 1 (θ → 0) なので、θ が限りなく 0 に近づくとき、間に挟まれた sin θ/ θ は、1 に近づくと言わざるを得ないのである。すなわち、 sin θ/ θ → 1 (θ → 0) となるのである。 ところで、ある人物について、 「人以上でもなく人以下でもない」 と評することがある。おそらく言わんとすることは、「同じ人間である」 という意味だとは思う。だが数学的には、「以上」 には、それ、またはそれより大きいという意味がある。よって、「人以上ではない」 ということは、人ではなく、かつ人より大きくない(上ではない、優れてはいない)、ということである。「以下」 についても同様である。であるから、 「人以上でもなく人以下でもない」 ということは、いったいその人物は、何だ? ということになってしまう。 まあそれは冗談だとしても、先の cos θ < sin θ/ θ < 1 および cos θ → 1 (θ → 0) から、sin θ/ θ → 1 (θ → 0) とすることにはちょっと疑問がある向きもあると思う。 つまり、 sin θ/ θ が 1より大きく、かつ1より小さいというのはおかしいではないか? この疑問に対しては、次のように説明できる。 θ≠0 なら、 cos θ < sin θ/ θ であっても、θ → 0 の極限では、 cos θ も sin θ/ θ も共に限りなく1に近づくのである(下グラフ参照)。 共に同じ時代を生きたライバルがいて、生きている間には、そのライバルに一度も勝てたことがなかったとしても、共に切磋琢磨していれば、死んで行く先はおよそ同じところである、というようなことであろうか。 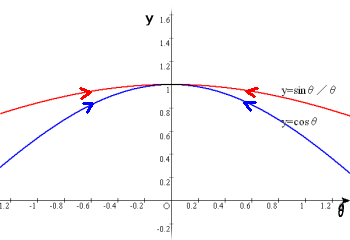
つまるところ、人は皆、同じ人として生まれ、死んで同じところに行く、ということであろうか。 (2002. 3.17)
|
関数 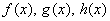 について、 について、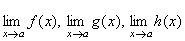 の極限値が存在し、 の極限値が存在し、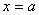 の近傍(x≠a)で、 の近傍(x≠a)で、不等式 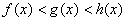 が成立し、かつ が成立し、かつ 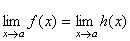 であるならば、 であるならば、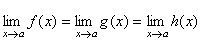 である。 である。 |
**********************************************************************************
Copyright(C) Yokahiyokatoki
 > 『数学的思考(?)エッセイ』 の試み
> 『数学的思考(?)エッセイ』 の試み