世の中は一筋縄？

　夏休みの季節である。我々教師には特に夏休みがあるわけではないが、この期間は授業がないこと、学生が質問に殆ど来なくなることで、時間ができるのはありがたい。ただし、「あれもこれも夏休みに」ということで先送りにしている事が溜まりに溜まっているのはいつものことである。「夏休みにゆっくり考えよう」などとはけっして思わないほうが賢明であることは、実証済みである。

　「授業中に居眠りなんかしたりしてあまり熱心に勉強しなかったので、この夏休みの間に自分で勉強して遅れを取りかえすぞ、と考えている人は手を挙げてみてください。」
というと、何人かの学生が手を挙げる。
　「実は私も皆さんの頃には、日頃はあまり勉強をしていなかったので、夏休み中は一人で猛勉強してやろう、とよく考えたものです。気持ちはよくわかります。ですがそれは無理です。そういうことは考えないほうがいいです。絶対できません。わたしが保証します。諦めましょう。」
ということにしている。授業中に集中できない者が、このくそ暑い夏休みの自由で何の束縛も刺激もないのに、一人で集中して勉強に取り組めるはずがないのは明らかである。私の言葉に反発して猛勉強し、「反例」を示すものが一人でも現れれば、それは嬉しい誤算である。

　計画を立てるのは好きだったから、毎年夏休みの始めにはきっちりと勉強の計画も立てるのだが、ほとんど教科書を開くことなどした例（ためし）がなかった。こういうことでは却って精神上よくないと考えた高校２年生の私は、その年の夏休みには「いっさい教科書は開かない」という計画を立てて見事に (？) 実行した。（ただし、我が校は今年度からは夏休みが開けたらさっそく定期試験が始まる。学生は教科書を開かないで過ごすわけには行くまい。なかなか世の中の実際は、一筋縄ではいかないものである。）

　「何もしない」というのは、これはこれでまた不安で精神上よくないものである。そこで、「ひとつだけ自分の好きなことについての自由研究をしよう」と取り組んだのが「反射望遠鏡の球面収差がない面の形」　についてである。生まれ育った所は広島県の中国山地の麓（ふもと）で、周りは低い山々に囲まれてはいたがその狭い夜空には星が降るほど輝いていた。その夜空を望遠鏡で覗いてみたいと思っていたのだが、できることなら自分で設計した自作の反射望遠鏡で毎晩月や星を観測できたらいいなあと密かに考えていたのである。その手始めとしての研究課題であった。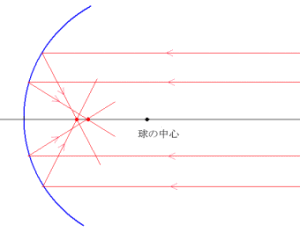

　もし反射面が球面であったら、左図のように平行に入ってきた光は一点に集まらない。これを球面収差という。これでは星はぼやけてしまい望遠鏡には使えない。ではどのような反射面なら光が一点に集まるか？　ということに興味をもったわけである。答えは調べれば分かることであろうが、自分で考えてみようと思ったのである。

　そして、「この式を解けば面の形が分かる」というところまでたどり着いたのだが、当時の私には解けそうにない式であった。そこで、夏休みで帰省していた大学生の兄に見せた。
　「これは確か微分方程式というものだが、わしには解けん。理系の大学に行けば習うじゃろう。」
なるほど兄は文系であった。そこで私の研究はストップしてしまったのである。

　何年か前、あるクラスでこの話をしたら、数日後一人の学生が「先生、できました。」といって見せに来た。まだ授業で微分方程式は教えてはいなか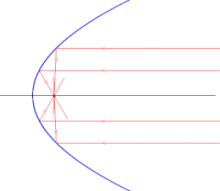

ったが、ちゃんと正しい解を得ていた。実は、平行に入ってきた光線が一点(焦点)に集る面は、放物線を回転してできる回転放物面（パラボラ）である。BSアンテナとして屋根に取り付けられている鍋のようなあれである。放物面が平行に入ってきた光線を一点(焦点)に集めることを示すのは簡単であるが、この逆を行うことは微分方程式を知らない学生にはちょっとむずかしい。さすが我が校には数学の得意な学生がいる。

　反射鏡を回転放物面にすると球面収差はなくなるが、今度はコマ収差が生じる。その他にも種々の収差などがあり実際の望遠鏡ではいろいろと複雑な工夫が必要であることを知ったのはずっと後のことである。
　なかなか世の中の実際は、一筋縄ではいかないものである。

(2002. 7.24)

　▲

　”放物線の形” はひとつしかない、ということをご存知であろうか。 (Ｉ) と (ＩＩ) とでは明らかに違うではないかと思われるかも知れないが、ひとつの放物線をどのスケールで描くかの違いなのである。 ( (Ｉ) の頂点の付近を拡大したら (ＩＩ) になる。）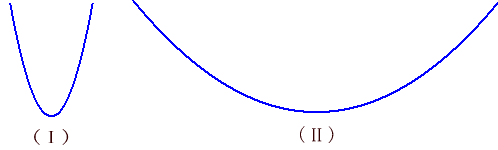

　岡部恒治著「数学はこんなに面白い」（日本経済新聞社）の本でこのことを知った。言われてみれば、なるほどそうだ。考えてみれば ”直線の形” はひとつしかない、 ”正三角形の形” もひとつしかない、 ”円の形” もひとつしかないのと同じように、 ”放物線の形” はひとつしかないのである。　同様に ”直角双曲線の形” もひとつしかない。　他方、 ”楕円の形” や ”双曲線の形” はひとつではなく無限にある。

　”放物線の形” はひとつしかないことを以下に示す。放物線を表す式は、ｙ＝ａｘ²＋ｂｘ＋ｃ（ａ≠０）であるが、この形は　ｙ＝ａｘ²　と同じである。また、ｙ＝ｂｘ²　（ｂ≠０）の放物線において、ｘ、ｙともｋ倍すると結局、ｙ＝ｋｂｘ²　となるので、ａ＝ｋｂとなるようにｋを選べば　ｙ＝ａｘ²　になる。すなわち、ｙ＝ｂｘ²　のグラフは　ｙ＝ａｘ²　のグラフを縦横とも　ａ／ｂ倍したものでしかない。

　物を放り投げたら放物線を描く。投げる角度によって描く曲線は違って見えるが、どれだけ離れて見るかの違いでしかないということである。世の中、意外と一筋縄である。

**********************************************************************************
Copyright(C)　Yokahiyokatoki