|
ウィスキーの 「ネイピア割り」 というものをご存知だろうか。初めて聞いたといわれるにちがいない。たったいま私が名づけたものだからである。 この 「ネイピア割り」 は作るのに手間がかかるし、しかも作る前から悪酔いしそうだと言われそうな代物だからあまり人にはお勧めしないが、数学をこよなく愛する暇な人種にはけっこう受け入れられるのではないか、と密かに思っている。といっても特に変わったものではなく、気が付かなければ(気が付いても)普通の水割りなのであるが…。 「ネイピア割り」 の作り方: 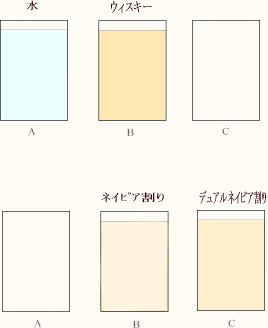 ① 同じ大きさのコップを3つ(A,B,Cとする) を用意し、Aには水を、Bにはウィスキーを入れる。ただし、水とウィスキーの量は同じにし、なみなみと注がないで、ほんの少しだけ余裕をもって注いでおくこと。
① 同じ大きさのコップを3つ(A,B,Cとする) を用意し、Aには水を、Bにはウィスキーを入れる。ただし、水とウィスキーの量は同じにし、なみなみと注がないで、ほんの少しだけ余裕をもって注いでおくこと。② ウィスキーのコップがなみなみになるまで、Aのコップの水を加えてよくかき混ぜた後、いま加えたのと同じ量分だけを、空のコップCに移す。 ③ 以下②でやったことを何回か繰り返し、Aの水のコップが空になるまで行う。 ④ そうすると手元には、B と C のコップにウィスキーの水割りができる。 B の方の水割りが 「ネイピア割り」 といわれるものである。 ちなみに C の方は 「デュアルネイピア割り」 という。 ちょっと計算してみればわかるが、この 「ネイピア割り」 のウィスキーと水の割合はおおよそ、 ウィスキー:水=1/e : 1-1/e =0.37:0.63 である。 最初、ウィスキーをなみなみと注がないで、ほんの少しだけ余裕をもって注いでおいたが、この余裕の部分の体積を限りなく 0 にすればその極限として、厳密にこの比で表される割合のものができあがるのである。この式で現れた e はネイピアの数(あるいは自然対数の底)といわれるもので、e=2.7182… であるが、こんなところにネイピアの数が顔を出すのがおもしろい。 もちろん 「デュアルネイピア割り」 ではこの割合が逆になったものができるので、こちらは濃い目のものがお好みの人向きである。 ところで、ウィスキーの水割りについて、ウィスキーと水との容積比は 1: 2 とするのが最適であるということを、数学的に証明(?)している方がいる(数学セミナ-1991年8月号p.6 芦ヶ原伸之著)。 吉村明という方で、その人によると、 ウイスキ-の量を x、水の量を y とする。このとき ウイスキ-を水で割る。すなわち、x÷y ウイスキ-に水を加える。すなわち、x+y ウイスキ-に水を掛ける。すなわち、x×y 上の3つは全く同じことを意味しているので、次の式が成立しなければならない。 x÷y=x+y=x×y この連立方程式を解けば、 x=0.5、 y=-1 を得る。 さて、このあとが少々苦しいのだが、 ÷、+、× を使っておいて - だけ使わないのは不公平だからその貴重な - を y に作用させて x : y=1: 2 が得られる。 これも悪酔いしそうな論法であるが、私はこのようなことを考えながら一杯やるのが好きである。 ところで、先ほどの 「ネイピア割り」 のウィスキーと水の割合をよく見ると、 ウィスキー:水=0.37:0.63≒1:2 ではないか。これは吉村氏による結論と同じだ、というにはやっぱり無理があるか? (2002. 8. 9)
|
つぎたす水の量を 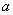 、最初のウィスキーの量を 、最初のウィスキーの量を 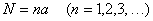 とする。ただし、 とする。ただし、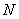 は一定とするので、 は一定とするので、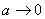 とすることは、 とすることは、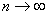 とすることになる。さて、 とすることになる。さて、
1回目の操作後のウィスキーの量は 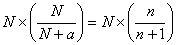 2回目の操作後のウィスキーの量は 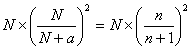 … 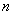 回目の操作後のウィスキーの量は 回目の操作後のウィスキーの量は  となる。よって、 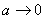 において、すなわち において、すなわち 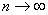 において、 において、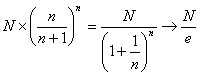 となる。 となる。また、次のように考えることもできる。時刻 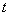 におけるコップBのウィスキーの量を におけるコップBのウィスキーの量を 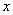 とし、時刻 とし、時刻 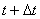 におけるウィスキーの量を におけるウィスキーの量を 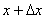 とすると、 とすると、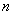 は大きいとして は大きいとして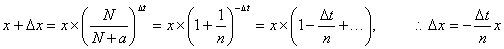 よって、  となる。この微分方程式を、初期条件 となる。この微分方程式を、初期条件 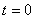 のとき のとき 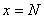 として解いて として解いて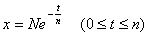 を得る。これより、 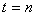 のとき、 のとき、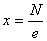 となる。 となる。部屋の空気を徐々に入れ替える場合などにも、同じ手法が使える。 |
**********************************************************************************
Copyright(C) Yokahiyokatoki
 > 『数学的思考(?)エッセイ』 の試み
> 『数学的思考(?)エッセイ』 の試み