|
熱き愛も時とともに冷ゆる。冷えゆく歩合の大きさは、その愛の大きさゆえにあり。それがこの世の生業(なりわい)なり。 愛の大きさ 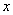 はある時 はある時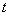 のもの。刹那(せつな)の時 のもの。刹那(せつな)の時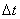 なれど、過ぎ去りてみれば愛は なれど、過ぎ去りてみれば愛は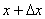 となりにけり。悲しきかな となりにけり。悲しきかな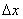 が負であることは何人たりとも如何ともしがたし。かのNewton の 「冷却の法則」 によれば が負であることは何人たりとも如何ともしがたし。かのNewton の 「冷却の法則」 によれば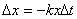 ( (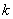 は正の定数) は正の定数)にて表わさるべし。 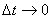 の極限に思いをはせれば、微分方程式 の極限に思いをはせれば、微分方程式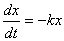 なるものを得る。ああ全てはこの方程式にて事は過ぎ行くのみ。 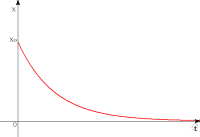 初期
初期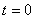 のむつまじし頃、愛の大きさはそれこそ測りがたき のむつまじし頃、愛の大きさはそれこそ測りがたき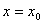 ほどもありしものを、この方程式を解くと ほどもありしものを、この方程式を解くと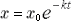 とあい成りにける。 様は左様のごとくなれば、すべてはこの世の定めと、時の流れに身をまかせざるを得ず 。 (2002. 8.10)
|
|
それにしても、なぜ 「Newtonの冷却の法則」 が成り立つのだろうか。「愛」 については、扱うには問題が複雑すぎて私の能力を超えているので、ここでは湯の温度について考察してみよう。 時間 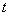 における湯の室温との温度差を における湯の室温との温度差を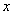 とすると、「Newtonの冷却の法則」 によれば とすると、「Newtonの冷却の法則」 によれば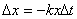 ( (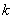 は正の定数) …(A) は正の定数) …(A)より、微分方程式 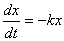 が成り立つということになるのであるが、(A)式がどのようにして得られるか、について考察しようというのである。 本来、湯の温度を決定しているものは、水分子の運動の激しさの度合いである。水分子が周りの空気や器の分子と衝突してその運動エネルギーを失うことにより、湯の温度が下がる。 いま水分子の総数をNとし、簡単のために全てが同じ速さで運動しているとする。そのうち単位時間につきn個の分子が周囲と衝突して速さを減少させ、そのn個分だけが室温に下がるとする。ということはこのn個分だけを、室温の湯で入れ替えるということになる。このために湯全体の温度が 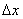 だけ変化するとすると、単位時間後の湯の温度 だけ変化するとすると、単位時間後の湯の温度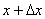 は、 は、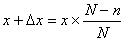 (前のエッセイ 『ネイピア割り』 参照)。したがって、 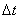 時間後の湯の温度 時間後の湯の温度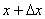 は は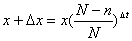 となる。 上式の右辺は 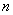 << <<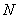 なので なので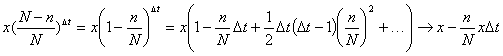 となり、 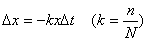 を得るのである。 湯の温度の下がる割合は、周りの室温との温度差に比例するというのが 「Newtonの冷却の法則」 であるが、もうひとつの要素である 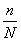 の値、すなわち湯の周りとの触れ合う面積にも比例するということも 「Newtonの冷却の法則」 である。 の値、すなわち湯の周りとの触れ合う面積にも比例するということも 「Newtonの冷却の法則」 である。
|
**********************************************************************************
Copyright(C) Yokahiyokatoki
 > 『数学的思考(?)エッセイ』 の試み
> 『数学的思考(?)エッセイ』 の試み