文一郎 : よう、数太郎。元気ないみたいだな。ついに彼女に振られたか。まあそれもよき人生勉強。女は彼女だけではない。元気をだせ。
数太郎 : いや、そうじゃあないんだけど。どうも彼女の気持ちがわからなくて…。 文一郎 : なに、彼女の気持ちがわからない? そんなら彼女に訊いてみればいいじゃあないか。 数太郎 : そう簡単に言うなよ。おれは真剣なんだ。そんなにズバッと訊けないよ。 文一郎 : そうか。そんなら、徐々に核心に近づいて行くんだな。 数太郎 : 例えば? 文一郎 : そうだな、まあ最初は、映画に誘う。次は夜の公園でデートをする。次は彼女の家に行って部屋に入れてくれるかどうか反応をみる、そしてだな…」 数太郎 : そう調子よくいくもんかよ。他人事だとおもって…。 文一郎 : やってみなけりゃわからんだろうが、やってみなけりゃ。 というわけで、数太郎は文一郎に背中を押されて、徐々に徐々に徐々に彼女に近づいて行く作戦に出たのでありました。 ところが、世の中そんなに甘いもんではありません。文一郎の言うように、トントン拍子に行くわけがありません。すんなり行ったかと思えば難所あり、もはや駄目かと諦めかければ思わぬ光明。文字通り、山あり谷ありのパターンであります。 文一郎 : よう、数太郎。少しは元気になったみたいだな。さては彼女を射止めたか? おれに少しは感謝しろよ。 数太郎 : いや、まだまだだが見込みはないことはなさそうなのだ。これを見てくれ。 といって差し出したのは、さすが数太郎のやりそうなこと。 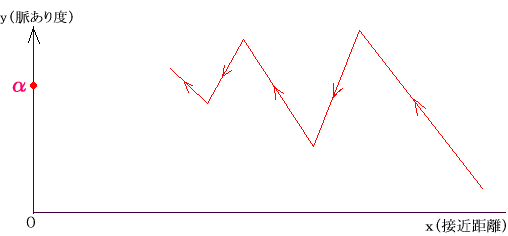
文一郎 : なんだこりゃ?
数太郎 : だから見てわかるように、おれの彼女接近距離 x に対する彼女の脈あり度 y だ。このグラフの示すように、必ずしも順風とは行っていないが、ある値 α に落ち着きそうなのがわかる。 文一郎 : 数太郎、おまえ何を一人でにやにやしながらつぶやいておるのだ。気は確かか? 数太郎 : 極めて確かだ。うん、間違いない。 ところが、グラフをにやにやして眺めていた数太郎、急に顔色が青ざめてきたのであります。 文一郎 : どうかしたのか、数太郎。今日は帰って寝ていた方がいいんじゃあないか。 数太郎 : いや、このグラフは、おれが彼女に限りなく近づくならば彼女の脈あり度は限りなくこの一定の値 α に近づく、ことを示しているように思うのだが…。 文一郎 : 数太郎がそう思うなら、それでいいじゃあないか。 数太郎 : だけど、限りなく近づくということは、どういうことだろう? 文一郎 : ははーん。限りなく近づくということは、限りなく近づけるだけで、永久に彼女とは合体できないということか。はっはっは! 数太郎 : いや、そういうことではないんだ。それに人の深刻な悩みを笑ってほしくない。 文一郎 : じゃあ、何が心配なのだ。 数太郎 : やっぱり、限りなく近づくということはどういうことなのか、をはっきりさせないと、おれの未来は見えてこないような気がする。グラフをよく見てくれ。おれが彼女に近づくとそれにともなって、彼女の脈あり度はすんなりある値に近づいているわけじゃあない。だから、この先ひょっとして彼女の心が大きく変わることがあるかも知れない。 文一郎 : そりゃそうだろう。そんなことは当たり前だ。女の気持ちと秋の空というじゃあないか。そんなことを心配していてもしかたがない。数太郎、やっぱり帰って寝て頭を冷やした方がいい。じゃあな。 その数日後、いたたまれなくなった数太郎は、彼女に次のような内容の手紙を書いて渡したのでありました。 「僕のあなたへの思いは日に日につのります。 僕のあなたへの接近距離 x に対するあなたの僕への脈あり度を y(x) とします。ある値 α があって、任意の ε>0 に対して、適当な δ>0 をとれば、|x|<δ、x≠0 ならば、常に |y(x)−α|<ε が成立するかどうか、確認したいのです。」 それから数年が経過したのでありますが、その後の数太郎の恋の結末を知る者はだれもいないのであります。 (2002.10.27)
|
[ε-δ 論法]
関数 f(x) が、x=x0 の近傍で定義されているとする。ある数 α があって、任意の ε>0 に対して、適当な δ>0 をとれば |x− x0|<δ、x≠x0 ならば、常に |f(x)−α|<ε が成立するとき、 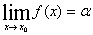
とかき、x →x0 のとき、f(x) の極限値は α であるという。
|
**********************************************************************************
Copyright(C) Yokahiyokatoki
 > 『数学的思考(?)エッセイ』 の試み
> 『数学的思考(?)エッセイ』 の試み