クローン人間計画があるという。人間は科学技術という名のもとに何か気味の悪いことをやり始めたのではないか、ついに人間が手を出すべきではない領域にまで立ち入ってしまったのではないかという不安や困惑は誰の胸にもあるだろう。
例えば、原子炉やダイオキシン、あるいは地球温暖化などなどの問題に対して、何らかの判断ができるだけの正確な知識を持ち正しい理解をしたいと願いながらも、それが極めて困難なほど専門的になり、我々はただただ専門家の言うことを信じるしかないという状況になりつつある。これはこれでゆゆしき問題であるが、ことが人間の遺伝子操作に関わる問題は、科学技術がどうのこうのという以前に本能的に拒否反応を示すのは私だけではないだろう。 それはさておき、あることがらに対して科学的説明がきちっとなされていて、その意味においては反論の余地のないものであっても、なぜか受け入れられないということがあるものである。なぜだろう。 その理由としてまず考えられるのは、科学的説明の前提となっていることがほんとうに確信のもてることなのかどうか、ということがある。自分がそのことがらに関しての十分な知識を持っていないためであるなら、自分で必要な勉強をせざるを得まい。 次に考えられる理由として、説明に用いられている論理の展開が本当に正しいのかどうか、ということである。これについても自分の頭で納得するまで考え検証するしかあるまい。 また、そうは言っても誰にも予期せぬ事が起こるかも知れない、という不安がある。確かに人間の知恵はすごいようでも思いもよらぬことがしばしば発生するものである。しかしながら、100%大丈夫だということはあり得ないことだし、誰にも予期できぬことであるからこそこれはどうしようもない。これを言い出したら、何もしないで今のままを続けるしかあるまい。 さらに、生き方の価値観や倫理観に根ざすこともあろう。あるいは、好き嫌いには理由はいらない。こうなってくると、科学的説明は無力である。 ここで、簡単な実験をしてみたい。次のような場合あなたならどうしますか? 【実験1】 あなたはもう人生をやり直せるほど若くはない。あなたの全財産は1,000万円あり、贅沢はできないけれど家族の生活は人並みのことはできているし、これからもほどほどの生活はできそうだ。 あるとき、次のような話が転がり込んできた。 『一枚のコインを投げて、あなたの大切な全財産1,000万円と、2億円との賭けをしませんか。 コインの表がでたら2億円はあなたのものです。 コインの裏がでたらあなたの全財産は取り上げられます。 勝つ確率は1/2です。もちろん、この賭けは1回切です。』 さて、あなたはどうしますか。 期待金額が1億円の賭けが 1,000万円でできるのであるから、数学的には絶対損のない賭けである。論理ではこの賭けに乗らない人はいないはずであるが。 論理的・科学的に考えることを否定するのではない。そうではなく、論理や科学に判断させることはできない、ましてや論理や科学そのものに判断能力はないということである。少なくとも人間である私はそうでありたいと思う。ロボットやクローン人間が当たり前になるかも知れない未来は、… 知らないが。 … と言いながら、あくまで数学的に考えてみようというのがこのエッセイである。 ○当選金:K(円) (0<K) ○当選確率:p (0<p<1) ○賭けの参加費:a(円) (0≦a≦K)(参加は1回のみ) という賭けがあったとする。 自分の全財産はA(円)である。 この賭けの期待金額はpK(円)である。したがって、確率的には a<pK であれば賭けに参加すべきであるという判断になる。 だが、問題は自分の全財産A(円)に対する参加費a(円)の割合と、自分の全財産A(円)に対する当選の期待金額 pK(円)である。 そこで、合理的に賭けに参加すべきかどうかを数値で表そうというのである。 ・a/A=0 のとき、当選確率pによらず必ず賭けに参加すべし(たとえ賭けに負けても自分は損をしないのだから)。 ・a/A=1 のとき、当選確率pによらず賭けに参加しない(いくらなんでも全財産を賭けるわけにはいかない)。 ・0<a/A<1 のとき、賭けに参加するかどうかは当選確率pによって定める。 ということを基準にしいろいろ考えた結果、賭けに参加すべき確率 X に対して、次の式を提案したい。 賭け参加率の方程式 (判断方程式) 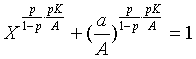 あるいは あるいは 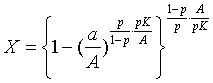 上式をグラフにすると次のようになる。 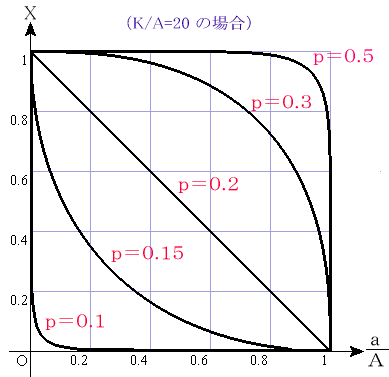
実験1の場合にこの式を適用してみよう。
K=2億円、p=1/2、a=1,000万円 A=1,000万円 なので、A=a で 賭けに参加すべき確率 X=0 となるのは当然であるが、もし a=800万円 で賭けに挑戦させてもらえるなら、左図において p=0.5 の曲線で a/A=0.8 の位置、すなわち X=0.98870 の確率でこの賭けに乗るべしという判断結果を得る。 この結論をどう受け止めるか。どこまでいってもやはり、最後の判断は自分でするしかなさそうだ。 よかったよかった …。 (2002.12.31 よいお年をお迎えください。)
|
**********************************************************************************
Copyright(C) Yokahiyokatoki
 > 『数学的思考(?)エッセイ』 の試み
> 『数学的思考(?)エッセイ』 の試み