福岡の今日の 6:00〜12:00 間の降水確率は 20% だと昨日のテレビで言っていたが、穏やかないい天気だ。このような天気を降水確率 20% の天気というのかなあ、と思いながら気持ちのよい正月をのんびり過ごしている。
それにしても、なんでもかんでも数値で表す時代になったものだ。ところが、この降水確率にしても、その意味を正確に理解している人はそう多くはいないと思う (私もよく知らない)。 だが、数値で表してもらうとわかった気分になれるし、おおよその天気は想像できるからそれで十分であるような気もする。 しかしながら、いくら降水確率が正確になったとしても、例えば降水確率 50% のとき傘を持って出かけるかどうかは、自分で判断しなくてはならない。 (もっとも降水確率が正確になった極限では 50% というようなことはありえなくて、0% か100% のどちらかになるのだろうか?) 科学技術や学問がどんなに進歩しても、物事の最後の判断はあくまで自分でするしかないということは、煩わしさというより、救いである。科学技術や学問は、判断に必要な情報を正確に得るための手段である。 … と思いながらも、正月休みの暇にまかせて、事の判断に対する方程式を考えてみた。 我々はある事をやろうか、それとも止めておこうかと考えるとき、基本的に次の3つのことを考慮して判断している。 p=成功する確率 ( 0 〜 1 の数値で表す) U=成功した場合の嬉しい度数 (成功したらどれだけ嬉しいかを 0 〜1 の数値で表す) D=失敗した場合のダメージ度数 (失敗したときどれだけのダメージかを 0 〜1 の数値で表す) そこで、これらを用いて事を行うべき確率 X を与える方程式として、次式を提唱する。 判断方程式 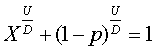 あるいは あるいは 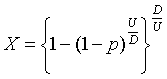
上式により、次のような自動判断機を作成してみた。
(注:この自動判断機使用による結果に対しその責任は負いません)
(2003. 1. 2 今年がよい年でありますように。)
|
【例】 あなたは視力が悪くなって、日常の生活をするにはほとんど不自由はないが、本を読んだりパソンコンをしたりはわずかしかできず、好きな車の運転などはできなくなったとする。 信頼できるお医者さんの説明では、手術をして成功すれば視力が完全に元に戻るが、失敗すれば失明することになる。 手術が成功する確率は 70% であるという。 さて、あなたはどうしますか? 成功する確率は p=0.7 であるが、ちなみに、 手術が成功した場合の嬉しい度数 U=0.8、 手術が失敗した場合のダメージ度数 D=0.99 として、自動判断機にかけてみると、 手術をおこなうべき確率は 56% と出てくる。さて、あなたはどうしますか? |
どんなに優れた自動判断機が完成したとしても、それが与えてくれるものはあくまで判断の情報であり、それをどのように解釈し最後の判断をするかは自分でしかない。物事の最後の判断はあくまで自分でするしかないということは、煩わしさというより、救いである。 … と思いながらも、正月休みの暇にまかせて、自動判断機が出した結果に対する判断基準を(正規分布を参考に)与えてみた。 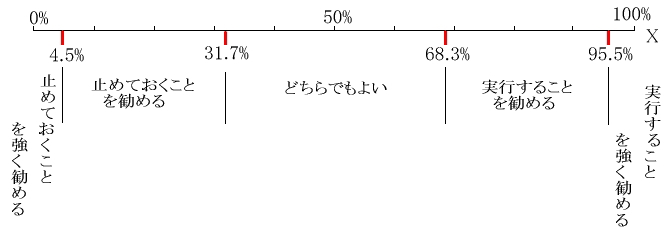 先の例だと、 手術をおこなうべき確率は 56% だったので、「どちらでもよい」 となる。さて、あなたはどうしますか? やはり、どこまでいっても切がない … 切がない … 切がない …。 |
**********************************************************************************
Copyright(C) Yokahiyokatoki
 > 『数学的思考(?)エッセイ』 の試み
> 『数学的思考(?)エッセイ』 の試み