> 『数学的思考(？)エッセイ』 の試み
人の評価は死んでからでないとわからないものだ、という。 何をもって人を評価するのがいいのかとか、人を評価すること自体に意味があるのかとか、さまざまな意見があるだろうが、よいわるい、意味があるなし、などということは別にして、基準さえきっちり定めておけば、人だろうが何だろうが評価はできる。 ただし、最終的には評価ができることでも、途中の段階で間違うことなく正しく評価することは極めてむずかしい、すなわち、ことが終わってからでないとその正しい評価はむずかしい、ということを話題にしたいのである。このよい例は、前回のエッセイで扱ったリバーシ（オセロ）というゲームである。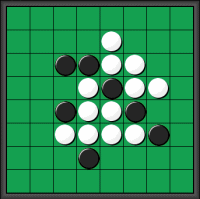 リバーシは、最終局面での石の数の多さを競うゲームであるから、勝敗は最終局面になってそれぞれの石の数を数えてみないとわからない。強い人は何手先も読むらしい
が、それにしても、例えば左図のような段階で、最終局面まで読み切ってどちらが勝つかが判定できる人はいないであろう。１秒間に数十万もの場合の数を試してみることができるコンピュータといえども、この場面から最終局面まで読みきることはできない。それほど場合の数が多いのである。 次は１６手目で白石の手番  上図の状況で、次は白石の手番である。白石を置くことができるのは、右図において青色で示した１２ヶ所である。これらのうちどこに置けば勝てるのかを、間違いなく判断したいのであるが、最終までには、まだおよそ４０手もある。それぞれの手で平均１０手あるとすると、１０40 もの場合を検討しなくてはならない。だから、最終局面まですべて試してみて勝敗を知ることはできない。したがって、現在のこの盤面で、あるいは２、３手打ってみた盤面を頭の中で描いて、次の最善手を決めなくてはならないのであるが、これらの途中盤面のどのような特徴に着目したらいいのかということが問題になるのである。 白石の置ける箇所は１２ヶ所 こいつは将来見込みがあるとかないとかを、現時点で判断しなければならないのであるが、現時点でのどの情報を重要視すべきかということが問題である。リバーシの場合には、いろいろな説が提唱されている。例えば、隅の石のように今後相手に絶対に返されない石（確定石）を増やす手がよいとか、自分の着手の選択肢（着手可能手数）が多くなるように、逆に相手の選択肢を減らすように打つのがよいとか、このことを簡単に数値化して計算できるようにした開放度理論とか、あるいは、勝ったゲームの途中で頻繁に現れるパターン（定石）があるのでこれを活用すべきであるとか、などなどである。これらはいずれも、多くの人たちの豊富な経験に基づいて必然的にできたものであるから、これらを習得すれば確実に誰よりも強くなれる。しかしながら、これが１００％絶対であるというものはない。やはり、すべてことが終わってからでないと絶対的に正しい判断はできないのである（将来はできるかも知れないが）。 このことから、次のような２つの意見が述べられる。 (A) リバーシでさえ、このようなものなのである。このことから、何かを現時点で評価するということが、いかに豊富な経験に裏打ちされた意見であろうと、その経験量は天文学的な場合の数の前では取るに足らないものであり、当てにならないものである。 (B) 天文学的な場合の数があろうとも、経験というものは、絶対的とはいえないまでも高い確率で正しい判断を可能にするものである。 どちらが正しい意見なのか、このことは、私が死ぬときになっても解らないだろう。 (2005.10.19) 人はどこまで読み切れるか？ (詰めリバーシ） CHECKMATE TERUBOY (HTML版） CHECKMATE TERUBOY (Java版） |