> 『数学的思考(？)エッセイ』 の試み|
成果の内の８割は２割の労力によって成される。 成果の残り２割を成すには８割の労力を要する。 表現はいろいろであるが、パレートの法則として知られているものである。 いろいろな方面で、この法則は適用される。 この法則を知ったら、完璧な成果をあげるために全精力を使ってくたくたになるより、わずか２割の労力で８割方の成果をあげたほうがよい、と考える人も多いと思う。 しかし、欲の無い私は８割もの成果は望まない。６割で生きていけるものならその方がいいような気もする。 ６割しか望まないなら、どれだけの労力でいいのだろうか、 ということが気になったので、 とりあえずちょっとだけ労力を使って計算してみた。 パレートの法則は、最終成果に対してばかりではなくどの段階でも常に成り立つものとし、労力 ｘ における成果を Ｆ(ｘ) とする。 横軸に労力、縦軸に成果をとって、この法則を表すグラフを描くと下図のようになった。 Ａ の成果をあげるために要する労力を ａ とするとき、 0.2ａ の労力で 0.8Ａ の成果が得られる。 Ａ は任意である。 この曲線の方程式は、 Ｆ(ｘ)＝0.8ｌｏｇ 0.2 ｘ で与えられる （下枠の導出参照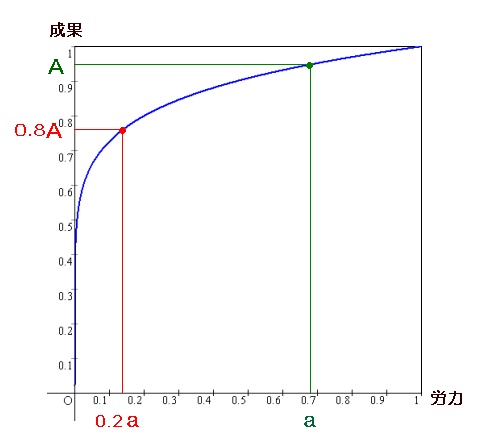）。  さて、６割の成果でよいなら、どれだけの労力でいいのか見てみよう。 上図のグラフでもだいたいのことはわかるが、 計算では Ｆ(ｘ)＝0.8ｌｏｇ 0.2 ｘ を逆に解いて、 ｘ＝0.2ｌｏｇ 0.8Ｆ(ｘ) となるので、 Ｆ(ｘ)＝0.8 であるためには ｘ＝0.2 Ｆ(ｘ)＝0.7 であるためには ｘ＝0.076 Ｆ(ｘ)＝0.6 であるためには ｘ＝0.025 うあー、ほんとかー！ ６割の成果でよいのならなんと、わずか 2.5％ の労力でいいんだ！ 生きることが楽しくなるぞー。 （注 ： ここでの結論は、パレートの法則を根拠なく拡張し、2.5% だけの労力を使って導いただけの完璧なものではないことに注意しましょう。 良い子の皆さんは、けっして私のように ６割で満足することのないように。 完璧をめざして最善を尽くしましょう。 光り輝く宝は、残りの２割にあることが多いからです。） (2006. 3.24)
|
（導出） 労力を ａ、成果を 関数 Ｆ(ａ) とすると、パレートの法則は Ｆ(0.2ａ) ＝ 0.8 Ｆ(ａ)、 Ｆ(0)＝0、 Ｆ(1)＝1 ということである。 これより、次式が得られる。 Ｆ(0.22 ａ) ＝ Ｆ(0.2×0.2ａ) ＝ 0.8 Ｆ(0.2ａ) ＝ 0.8×0.8 Ｆ(ａ) ＝ 0.82 Ｆ(ａ) 以下同様にして、 Ｆ(0.2ｎ ａ)＝0.8ｎ Ｆ(ａ) （ｎ＝1,2,3,…） となる。 ａ＝1 として、 Ｆ(0.2ｎ)＝0.8ｎ （ｎ＝1,2,3,…） を得る。 次に、 ｘ＝0.2ｎ あるいは、 ｎ＝ｌｏｇ 0.2 ｘ とおくと、 Ｆ(ｘ)＝0.8ｌｏｇ 0.2 ｘ を得る。 ｎは自然数なので、ｘ は離散的な値しかとらないが実数に拡張する。 |